Rho

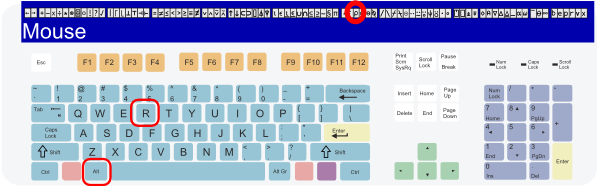
⍴ — Shape or Reshape — Keystroke ALT+r — Character 9076 or x2374

Note: This is ALT+r; ALT+SHIFT+R will generate the symbol root (√).

Rho may be used as a monadic or dyadic operator, depending on the functionality desired. Used monadically with the argument to the right returns the shape of the argument. Used dyadically, the argument on the left is used to reshape the argument on the right.

Shape

The symbol ⍴ used monadically with no left argument returns the shape of the argument to the right, i.e. the size or dimensions of a scalar, string, vector, array or matrix. Shape returns null for a scalar or a single character, it returns 0 for a null string, the length of a string of at least two characters, the number of elements of an array or vector, and the number of elements of a matrix.

Reshape

Z←L⍴R returns an array of shape L whose items are taken from R in row major order, repeated as necessary.

L is a scalar or vector of non-negative integers, and R is an arbitrary array.

If the right argument is empty, the result consists of ×/⍴L copies of the fill item of R.

For example, in origin-1

      2 3⍴⍳6
 1 2 3
 4 5 6
      2 3⍴⍳0
 0 0 0
 0 0 0

The idea for the latter enhancement was taken from Dyalog APL.

{{article footer}

See Also

NARS 2000 Lang Tool Bar

←

→

+

-

×

÷

*

⍟

⌹

○

!

?

√

|

⌈

⌊

⊥

⊤

⊣

⊢

≡

≢

<

≤

=

≥

>

≠

∨

∧

⍱

⍲

↑

↓

⊂

⊃

⌷

⍋

⍒

⍳

∊

⍸

⍷

∪

∩

⊆

⊇

~

§

π

..

,

⍪

⍴

⌽

⊖

⍉

/

\

⌿

⍀

⊙

¨

⍨

⍤

⍣

⍡

⍥

⍦

.

∘

⍠

‼

⌻

∂

∫

⍞

⎕

⍎

⍕

⋄

⍝

∇

∆

⍙

_

⍺

⍵

¯

⍬

∞

∅

Second Row

i j k

i j k l

g

p

r

v

x