Rho: Difference between revisions
(→Shape - Monadic {rho}: RhoRho = added rank examples) |
Sudleyplace (talk | contribs) No edit summary |
||
| Line 14: | Line 14: | ||
==Shape - Monadic {rho}== | ==Shape - Monadic {rho}== | ||
<big>Symbol '''{rho}''' when used '''monadically''' (no left argument) returns the '''shape of {rho}'s right argument''', i.e. the size or dimensions of a scalar, string, vector, array or matrix. Shape returns null for a scalar or a single character, it returns 0 for a null string, the length of a string of at least two characters, the number of elements of an array or vector, and the number of elements of a matrix.</big> | <big>Symbol '''{rho}''' when used '''monadically''' (no left argument) returns the '''shape of {rho}'s right argument''', i.e. the size or dimensions of a scalar, string, vector, array or matrix. Shape returns null for a scalar or a single character, it returns 0 for a null string, the length of a string of at least two characters, the number of elements of an array or vector, and the number of elements of a matrix.</big> | ||
<pre> | <apll><pre> | ||
⍴ 1 2 3 4 5 6 ⍝ Rho in the case of vectors represents a Count(# elements) function | ⍴ 1 2 3 4 5 6 ⍝ Rho in the case of vectors represents a Count(# elements) function | ||
6 | 6 | ||
| Line 20: | Line 20: | ||
7 | 7 | ||
⍴ 1 ⍝ For a scalar right argument, Rho generates a null vector. | ⍴ 1 ⍝ For a scalar right argument, Rho generates a null vector. | ||
⍴⍴ 1 ⍝ The shape of the shape(⍴⍴) of a scalar (because the shape of a scalar is a null) - generates zero. | ⍴⍴ 1 ⍝ The shape of the shape(⍴⍴) of a scalar (because the shape of a scalar is a null) - generates zero. | ||
0 | 0 | ||
⍴ 'a' ⍝ Ditto for {numbers, integers, letters}, etc. - for scalar right arguments: Rho also generates a null vector. | ⍴ 'a' ⍝ Ditto for {numbers, integers, letters}, etc. - for scalar right arguments: Rho also generates a null vector. | ||
⍴⍴ 'a' | ⍴⍴ 'a' | ||
| Line 44: | Line 41: | ||
⍴⍴(⍳6) ⍝ Monadic leftmost {rho}{rho} generates the RANK of the vector = 1 (vector) | ⍴⍴(⍳6) ⍝ Monadic leftmost {rho}{rho} generates the RANK of the vector = 1 (vector) | ||
1 | 1 | ||
</pre> | </pre></apll> | ||
==Reshape - Dyadic {rho}== | ==Reshape - Dyadic {rho}== | ||
| Line 69: | Line 66: | ||
</table> | </table> | ||
<br /> | <br /> | ||
<p>For example, in origin 1(where ⎕IO=1)</p> | <p>For example, in origin <apll>1</apll> (where <apll>⎕IO=1</apll>)</p> | ||
<apll> | <apll><pre> | ||
2 3⍴⍳6 | |||
1 2 3 | |||
4 5 6 | |||
2 3⍴⍳0 | |||
0 0 0 | |||
0 0 0</pre></apll> | |||
<p>The idea for the latter enhancement was taken from Dyalog APL.</p> | <p>The idea for the latter enhancement was taken from Dyalog APL.</p> | ||
| Line 85: | Line 83: | ||
==See Also== | ==See Also== | ||
{{Language Toolbar}} | {{Language Toolbar}} | ||
[[Category:Mouse Group 8|R]] | [[Category:Mouse Group 8|R]] | ||
[[Category:Symbols|R]] | [[Category:Symbols|R]] | ||
Revision as of 23:11, 15 April 2018
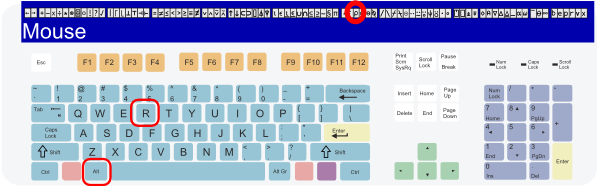
⍴ — Shape or Reshape — Keystroke ALT+r — Character 9076 or x2374
Note: This is ALT+r; ALT+SHIFT+R will generate the symbol root (√).
Rho may be used as a monadic or dyadic operator, depending on the functionality desired. Used monadically with the argument to the right returns the shape of the argument. Used dyadically, the argument on the left is used to reshape the argument on the right.
Shape - Monadic ⍴
Symbol ⍴ when used monadically (no left argument) returns the shape of ⍴'s right argument, i.e. the size or dimensions of a scalar, string, vector, array or matrix. Shape returns null for a scalar or a single character, it returns 0 for a null string, the length of a string of at least two characters, the number of elements of an array or vector, and the number of elements of a matrix.
⍴ 1 2 3 4 5 6 ⍝ Rho in the case of vectors represents a Count(# elements) function
6
⍴'abcdefg' ⍝ Similarly with text strings(vector of chars), Rho represents a Count function
7
⍴ 1 ⍝ For a scalar right argument, Rho generates a null vector.
⍴⍴ 1 ⍝ The shape of the shape(⍴⍴) of a scalar (because the shape of a scalar is a null) - generates zero.
0
⍴ 'a' ⍝ Ditto for {numbers, integers, letters}, etc. - for scalar right arguments: Rho also generates a null vector.
⍴⍴ 'a'
0
⍴, 4.581 ⍝ Rho for a raveled(, or comma used) scalar(real num 4.581) - again correctly represents a Count(# elements) function
1
2 3⍴⍳6 ⍝ Dyadic call for demonstration purposes(see below for dyadic calls to ⍴): result = 2 rows and 3 cols matrix of integers(1..6)
1 2 3
4 5 6
⍴2 3⍴⍳6 ⍝ Monadic LEFTMOST shape ⍴ yields: matrix has 2 rows and 3 cols; equivalent to ⍴(2 3⍴⍳6) which has parentheses added for clarity
2 3
⍴⍴(2 3⍴⍳6) ⍝ Monadic LEFTMOST shape-shape or ⍴⍴ generates the RANK of the 2 row, 3 col matrix which = 2 (matrix)
2
⍴⍴(⍳6) ⍝ Monadic leftmost ⍴⍴ generates the RANK of the vector = 1 (vector)
1
Reshape - Dyadic ⍴
⍴'s Left Argument(L) output-reshapes ⍴'s Right Argument(R).
|
||||
| L is a scalar or vector of non-negative integers, and R is an arbitrary array. | ||||
| If the right argument is empty, the result consists of ×/⍴L copies of the fill item of R. |
For example, in origin 1 (where ⎕IO=1)
2 3⍴⍳6
1 2 3
4 5 6
2 3⍴⍳0
0 0 0
0 0 0
The idea for the latter enhancement was taken from Dyalog APL.
| See Also | ||
| System Commands | System Variables and Functions | Operators |
| Keyboard | ||||||||||||||
| A+S | ⍪ | ≡ | ≢ | ⍒ | ⍋ | ⌽ | ⍉ | ⊖ | ⍟ | ⍱ | ⍲ | ⍠ | ⌹ | |
| Alt | ⋄ | ¨ | ¯ | < | ≤ | ∅ | ≥ | > | ≠ | ∨ | ∧ | × | ÷ | |
| Sh | ~ | ! | @ | # | $ | % | ^ | & | * | ( | ) | _ | + | |
| Key | ` | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | - | = | |
| A+S | ⍷ | √ | ⍨ | ⍸ | ⍥ | ⍣ | ⍞ | ⍬ | ⊣ | |||||
| Alt | ? | ⍵ | ∊ | ⍴ | § | ↑ | ↓ | ⍳ | ○ | π | ← | → | ⊢ | |
| Sh | Q | W | E | R | T | Y | U | I | O | P | { | } | | | |
| Key | q | w | e | r | t | y | u | i | o | p | [ | ] | \ | |
| A+S | ∫ | ∂ | ⌻ | ⍢ | ⍙ | ⍤ | ⍫ | ⌷ | ||||||
| Alt | ⍺ | ⌈ | ⌊ | ∞ | ∇ | ∆ | ∘ | ‼ | ⎕ | ⍎ | ⍕ | |||
| Sh | A | S | D | F | G | H | J | K | L | : | " | |||
| Key | a | s | d | f | g | h | j | k | l | ; | ' | |||
| A+S | ⊆ | ⊇ | χ | ⍡ | ⍭ | ⊙ | ||||||||
| Alt | ⊂ | ⊃ | ∩ | ∪ | ⊥ | ⊤ | ⍦ | ⍝ | ⍀ | ⌿ | ||||
| Sh | Z | X | C | V | B | N | M | < | > | ? | ||||
| Key | z | x | c | v | b | n | m | , | . | / | ||||
| NARS 2000 Lang Tool Bar |
← | → | + | - | × | ÷ | * | ⍟ | ⌹ | ○ | ! | ? | √ | | | ⌈ | ⌊ | ⊥ | ⊤ | ⊣ | ⊢ | |||
| ≡ | ≢ | < | ≤ | = | ≥ | > | ≠ | ∨ | ∧ | ⍱ | ⍲ | ↑ | ↓ | ⊂ | ⊃ | ⌷ | ⍋ | ⍒ | |||||
| ⍳ | ∊ | ⍸ | ⍷ | ∪ | ∩ | ⊆ | ⊇ | ~ | § | π | .. | , | ⍪ | ⍴ | ⌽ | ⊖ | ⍉ | ||||||
| / | \ | ⌿ | ⍀ | ⊙ | ¨ | ⍨ | ⍤ | ⍣ | ⍡ | ⍥ | ⍦ | . | ∘ | ⍠ | ‼ | ⌻ | ∂ | ∫ | ⍞ | ⎕ | ⍎ | ⍕ | |
| ⋄ | ⍝ | ∇ | ∆ | ⍙ | _ | ⍺ | ⍵ | ¯ | ⍬ | ∞ | ∅ | ||||||||||||
| Second Row | i j k | i j k l | g | p | r | v | x | ||||||||||||||||
[[Category:Mouse Group {{{1}}}|{{{2}}}]]
See Also
| NARS 2000 Lang Tool Bar |
← | → | + | - | × | ÷ | * | ⍟ | ⌹ | ○ | ! | ? | √ | | | ⌈ | ⌊ | ⊥ | ⊤ | ⊣ | ⊢ | |||
| ≡ | ≢ | < | ≤ | = | ≥ | > | ≠ | ∨ | ∧ | ⍱ | ⍲ | ↑ | ↓ | ⊂ | ⊃ | ⌷ | ⍋ | ⍒ | |||||
| ⍳ | ∊ | ⍸ | ⍷ | ∪ | ∩ | ⊆ | ⊇ | ~ | § | π | .. | , | ⍪ | ⍴ | ⌽ | ⊖ | ⍉ | ||||||
| / | \ | ⌿ | ⍀ | ⊙ | ¨ | ⍨ | ⍤ | ⍣ | ⍡ | ⍥ | ⍦ | . | ∘ | ⍠ | ‼ | ⌻ | ∂ | ∫ | ⍞ | ⎕ | ⍎ | ⍕ | |
| ⋄ | ⍝ | ∇ | ∆ | ⍙ | _ | ⍺ | ⍵ | ¯ | ⍬ | ∞ | ∅ | ||||||||||||
| Second Row | i j k | i j k l | g | p | r | v | x | ||||||||||||||||