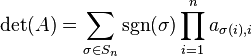Determinant Operator: Difference between revisions
m (WikiSysop moved page Determinant to Determinant Operator) |
Sudleyplace (talk | contribs) No edit summary |
||
| (4 intermediate revisions by one other user not shown) | |||
| Line 26: | Line 26: | ||
[[image:LeibnizFormula.png]] | [[image:LeibnizFormula.png]] | ||
<p>for an ''n''×''n'' matrix, where sgn is the [https://en.wikipedia.org/wiki/Even_and_odd_permutations sign function] of [https://en.wikipedia.org/wiki/Permutation permutation]s in the [https://en.wikipedia.org/wiki/Permutation_group permutation group] ''S''<sub>''n''</sub>, which returns +1 and −1 for [https://en.wikipedia.org/wiki/Even_and_odd_permutations even and odd permutations], respectively. The latter sum of positive or negative quantities is actually an alternating sum (<apll>-/</apll> in APL) and the righthand part is a product of terms (<apll>×</apll> in APL), hence this formula may be described as an alternating sum of products. This means that the usual determinant of a matrix is obtained via <apll>-.×</apll>. Moreover, the [https://en.wikipedia.org/wiki/Permanent permanent] of a matrix uses <apll>+.×</apll>.</p> | <p>for an ''n''×''n'' matrix, where sgn is the [https://en.wikipedia.org/wiki/Even_and_odd_permutations sign function] of [https://en.wikipedia.org/wiki/Permutation permutation]s in the [https://en.wikipedia.org/wiki/Permutation_group permutation group] ''S''<sub>''n''</sub>, which returns +1 and −1 for [https://en.wikipedia.org/wiki/Even_and_odd_permutations even and odd permutations], respectively. The latter sum of positive or negative quantities is actually an alternating sum (<apll>-/</apll> in APL) and the righthand part is a product of terms (<apll>×/</apll> in APL), hence this formula may be described as an alternating sum of products. This means that the usual determinant of a matrix is obtained via <apll>-.×</apll>. Moreover, the [https://en.wikipedia.org/wiki/Permanent permanent] of a matrix uses <apll>+.×</apll>.</p> | ||
< | <h2>Examples</h2> | ||
<apll> | <apll><pre> | ||
1 8 1 8 | ⎕←a←?4 4⍴10 | ||
5 1 7 2 | 1 8 1 8 | ||
6 3 9 4 | 5 1 7 2 | ||
4 9 8 8 | 6 3 9 4 | ||
4 9 8 8 | |||
26 | -.×a | ||
26 | |||
+.×a | |||
18886</pre></apll> | |||
<p>The Leibniz formula | <h2>Alternate Derived Functions</h2> | ||
<p>The Leibniz formula nicely allows us to substitute other functions for (<apll>-</apll>) and (<apll>×</apll>) to obtain alternate derived functions in order to solve different problems, while <b>still using the same basic algorithm</b>.</p> | |||
<p>One such alternate derived function is <apll>⌊.+</apll> which finds the [https://en.wikipedia.org/wiki/Assignment_problem lowest cost assignment] of agents (rows) to tasks (columns) where each agent is assigned one and only one task. For example,</p> | <p>One such alternate derived function is <apll>⌊.+</apll> which finds the [https://en.wikipedia.org/wiki/Assignment_problem lowest cost assignment] of agents (rows) to tasks (columns) where each agent is assigned one and only one task. For example,</p> | ||
<apll> | <apll><pre> | ||
⌊.+a | |||
10</pre></apll> | |||
<p>This result means that there is a minimal assignment of choices of an entry from each column and each row that sums to <apll>10</apll>, a result easily seen using another pair of operands to the Determinant Operator so as to display the actual choices:</p> | <p>This result means that there is a minimal assignment of choices of an entry from each column and each row that sums to <apll>10</apll>, a result easily seen using another pair of operands to the Determinant Operator so as to display the actual choices:</p> | ||
<apll> | <apll><pre> | ||
4 3 1 2</apll> | {(+/⍺)<+/⍵:⍺ ⋄ ⍵}.,a | ||
4 3 1 2</pre></apll> | |||
<p>That is, a minimal set of choices is the <apll>4</apll> in column <apll>1</apll>, the <apll>3</apll> in column <apll>2</apll>, the <apll>1</apll> in column <apll>3</apll>, and the <apll>2</apll> in column <apll>4</apll>, which, by construction, are all in different rows.</p> | |||
<p>Moreover, just as <apll>-.×</apll> uses an optimized algorithm ([http://www.gnu.org/software/gsl/manual/html_node/LU-Decomposition.html#LU-Decomposition LU Decomposition]), so does <apll>⌊.+</apll> ([https://github.com/maandree/hungarian-algorithm-n3/blob/master/hungarian.c Kuhn's Hungarian Algorithm]) as well as <apll>⌈.+</apll> and <apll>{(+/⍺)<+/⍵:⍺ ⋄ ⍵}</apll>, along with a number of variations of the latter anonymous function (e.g. <apll>{(+/⍺)>+/⍵:⍺ ⋄ ⍵}</apll>, <apll>{(+/⍺)<+/⍵:⍵ ⋄ ⍺}</apll>, etc.). Consequently, all of the above derived functions return results very quickly for reasonably large arguments. For example, <apll>⌊.+</apll> on a random <apll>50</apll> by <apll>50</apll> matrix takes only a few milliseconds.</p> | |||
<p>Another variant of the lowest cost assignment is <apll>⌊.×</apll> and <apll>⌈.×</apll>. Rather than treat these expressions specially, they can be resolved via the identities <apll>⌊.×R ←→ *⌊.+⍟R</apll> and <apll>⌈.×R ←→ *⌈.+⍟R</apll>. | |||
< | <h2>References</h2> | ||
< | <ol> | ||
<li>[http://www.jsoftware.com/papers/satn42.htm Determinant-Like Functions Produced by the Dot Operator], SATN-42 (Sharp APL Technical Notes), 1982-04-01, by K.E. Iverson</li> | |||
<li>[https://en.wikipedia.org/wiki/Leibniz_formula_for_determinants Leibniz Formula], from Wikipedia</li> | |||
<li>[https://en.wikipedia.org/wiki/Permanent Permanent], from Wikipedia</li> | |||
<li>[https://en.wikipedia.org/wiki/Assignment_problem Assignment Problem], from Wikipedia</li> | |||
</ol> | |||
Revision as of 23:51, 15 April 2018
|
||||
| R is a numeric scalar, vector, or matrix. | ||||
| f and g are functions. |
The determinant of a matrix is a value associated with it whose interpretation depends upon the purpose of the matrix. For example, where the matrix represents the coefficients in a system of linear equations, a non-zero determinant indicates that the system has a unique solution, and a zero determinant indicates that the system has either no solutions or many solutions. For the original source document that introduced this operator, see Determinant-Like Functions Produced by the Dot Operator.
There are many formulas that many be used to calculate the value of the determinant, one of which (from Wikipedia, due to Leibniz) is particularly suited to our purposes:
for an n×n matrix, where sgn is the sign function of permutations in the permutation group Sn, which returns +1 and −1 for even and odd permutations, respectively. The latter sum of positive or negative quantities is actually an alternating sum (-/ in APL) and the righthand part is a product of terms (×/ in APL), hence this formula may be described as an alternating sum of products. This means that the usual determinant of a matrix is obtained via -.×. Moreover, the permanent of a matrix uses +.×.
Examples
⎕←a←?4 4⍴10
1 8 1 8
5 1 7 2
6 3 9 4
4 9 8 8
-.×a
26
+.×a
18886
Alternate Derived Functions
The Leibniz formula nicely allows us to substitute other functions for (-) and (×) to obtain alternate derived functions in order to solve different problems, while still using the same basic algorithm.
One such alternate derived function is ⌊.+ which finds the lowest cost assignment of agents (rows) to tasks (columns) where each agent is assigned one and only one task. For example,
⌊.+a 10
This result means that there is a minimal assignment of choices of an entry from each column and each row that sums to 10, a result easily seen using another pair of operands to the Determinant Operator so as to display the actual choices:
{(+/⍺)<+/⍵:⍺ ⋄ ⍵}.,a
4 3 1 2
That is, a minimal set of choices is the 4 in column 1, the 3 in column 2, the 1 in column 3, and the 2 in column 4, which, by construction, are all in different rows.
Moreover, just as -.× uses an optimized algorithm (LU Decomposition), so does ⌊.+ (Kuhn's Hungarian Algorithm) as well as ⌈.+ and {(+/⍺)<+/⍵:⍺ ⋄ ⍵}, along with a number of variations of the latter anonymous function (e.g. {(+/⍺)>+/⍵:⍺ ⋄ ⍵}, {(+/⍺)<+/⍵:⍵ ⋄ ⍺}, etc.). Consequently, all of the above derived functions return results very quickly for reasonably large arguments. For example, ⌊.+ on a random 50 by 50 matrix takes only a few milliseconds.
Another variant of the lowest cost assignment is ⌊.× and ⌈.×. Rather than treat these expressions specially, they can be resolved via the identities ⌊.×R ←→ *⌊.+⍟R and ⌈.×R ←→ *⌈.+⍟R.
References
- Determinant-Like Functions Produced by the Dot Operator, SATN-42 (Sharp APL Technical Notes), 1982-04-01, by K.E. Iverson
- Leibniz Formula, from Wikipedia
- Permanent, from Wikipedia
- Assignment Problem, from Wikipedia