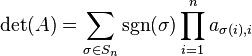Determinant Operator: Difference between revisions
(Created page with "<table border="1" cellpadding="5" cellspacing="0" rules="none" summary=""> <tr> <td> <table border="0" cellpadding="5" cellspacing="0" summary=""> <tr> <td val...") |
No edit summary |
||
| Line 40: | Line 40: | ||
18886</apll> | 18886</apll> | ||
<p>The Leibniz formula also allows us to substitute other functions for (<apll>-</apll>) and (<apll>×</apll>) to obtain alternate derived functions.</p> | <p>The Leibniz formula also allows us to substitute other functions for (<apll>-</apll>) and (<apll>×</apll>) to obtain alternate derived functions in order to solve different problems.</p> | ||
<p>One such alternate | <p>One such alternate derived function is <apll>⌊.+</apll> which finds the [https://en.wikipedia.org/wiki/Assignment_problem lowest cost assignment] of agents (rows) to tasks (columns) where each agent is assigned one and only one task. For example,</p> | ||
<apll> ⌊.+a<br /> | <apll> ⌊.+a<br /> | ||
10</apll> | 10</apll> | ||
<p>This result means that there is a minimal assignment of choices of an entry from each column and each row that sums to <apll>10</apll>, a result easily seen using another pair of | <p>This result means that there is a minimal assignment of choices of an entry from each column and each row that sums to <apll>10</apll>, a result easily seen using another pair of operands to the Determinant Operator so as to display the actual choices:</p> | ||
<apll> {(+/⍺)<+/⍵:⍺ ⋄ ⍵}.,a<br /> | <apll> {(+/⍺)<+/⍵:⍺ ⋄ ⍵}.,a<br /> | ||
4 3 1 2</apll> | 4 3 1 2</apll> | ||
<p>That is, the minimal set of choices is the <apll>4</apll> in column <apll>1</apll>, the <apll>3</apll> in column <apll>2</apll>, the <apll>1</apll> in column <apll>3</apll>, and the <apll>2</apll> in column <apll>4</apll>.</p> | <p>That is, the minimal set of choices is the <apll>4</apll> in column <apll>1</apll>, the <apll>3</apll> in column <apll>2</apll>, the <apll>1</apll> in column <apll>3</apll>, and the <apll>2</apll> in column <apll>4</apll>, which, by construction, are all in different rows.</p> | ||
<p>Moreover, just as <apll>-.×</apll> uses a specialized algorithm, so does <apll>⌊.+</apll> as well as <apll>⌈.+</apll> and <apll>{(+/⍺)<+/⍵:⍺ ⋄ ⍵}.,</apll> along with several of its variations, so those derived functions quickly return results for large arguments. For example, <apll>⌊.+</apll> on a <apll>50</apll> by <apll>50</apll> matrix takes only a few milliseconds.</p> | |||
Revision as of 16:45, 24 October 2013
|
||||
| R is a numeric scalar, vector, or matrix. | ||||
| f and g are functions. |
The determinant of a matrix is a value associated with it whose interpretation depends upon the purpose of the matrix. For example, where the matrix represents the coefficients in a system of linear equations, a non-zero determinant indicates that the system has a unique solution, and a zero determinant indicates that the system has either no solutions or many solutions. For the original source document that introduced this operator, see Determinant-Like Functions Produced by the Dot Operator.
There are many formulas that many be used to calculate the value of the determinant, one of which (from Wikipedia, due to Leibniz) is particularly suited to our purposes:
for an n×n matrix, where sgn is the sign function of permutations in the permutation group Sn, which returns +1 and −1 for even and odd permutations, respectively. The latter sum of positive or negative quantities is actually an alternating sum (-/ in APL) and the righthand part is a product of terms (× in APL), hence this formula may be described as an alternating sum of products. This means that the usual determinant of a matrix is obtained via -.×. Moreover, the permanent of a matrix uses +.×.
For example,
⎕←a←?4 4⍴10
1 8 1 8
5 1 7 2
6 3 9 4
4 9 8 8
-.×a
26
+.×a
18886
The Leibniz formula also allows us to substitute other functions for (-) and (×) to obtain alternate derived functions in order to solve different problems.
One such alternate derived function is ⌊.+ which finds the lowest cost assignment of agents (rows) to tasks (columns) where each agent is assigned one and only one task. For example,
⌊.+a
10
This result means that there is a minimal assignment of choices of an entry from each column and each row that sums to 10, a result easily seen using another pair of operands to the Determinant Operator so as to display the actual choices:
{(+/⍺)<+/⍵:⍺ ⋄ ⍵}.,a
4 3 1 2
That is, the minimal set of choices is the 4 in column 1, the 3 in column 2, the 1 in column 3, and the 2 in column 4, which, by construction, are all in different rows.
Moreover, just as -.× uses a specialized algorithm, so does ⌊.+ as well as ⌈.+ and {(+/⍺)<+/⍵:⍺ ⋄ ⍵}., along with several of its variations, so those derived functions quickly return results for large arguments. For example, ⌊.+ on a 50 by 50 matrix takes only a few milliseconds.