Derivative
|
||||||||
| L is an optional array passed as the left argument to every call to f. | ||||||||
| R is a Real numeric array. If R is a singleton, it represents the point at which the Derivative is calculated. If R is an array, it represents the multiple values at which the Partial Derivative is calculated. | ||||||||
| f is an arbitrary ambivalent function, returning a Real numeric array. |
Introduction
While working on the Matrix operator[1], I’ve found I needed a Numerical Differentiation (ND) operator in order to apply the Matrix operator to non-diagonalizable matrices. This operator uses Numerical Analysis methods to calculate the value of the Derivative of a function at a given point.
It may be used to calculate Nth order Derivatives as well as first order Partial Derivatives. The latter are calculated as per Iverson[2] and expanded upon by Powell[3].
Notation
The symbol chosen for this operator is Curly D (∂), entered from the keyboard as Alt-’D’ or Alt-Shift-'d' (U+2202), and used in mathematics for Partial Differentiation.
Examples
For example,
!∂0 ⋄ ¯1g1 ¯0.5772156649015197 ¯0.5772156649015329 !∂0 ⋄ 1g2+1p2÷6 1.9781119906525646 1.978111990655945
That is, exact value of the first derivative of the Factorial function at 0 is -γ, where γ is Gamma, the Euler-Mascheroni constant, and the exact value of the second derivative is γ2+π2/6.
In this and following examples, the rightmost of consecutive digits that all agree with the exact result is marked.
The derived function may be called dyadically, too:
X←0.6 ⋄ 1○∂X ⋄ 2○X
0.8253356149096904
0.8253356149096783
where the first derivative of the Sine function is the Cosine function.
Accuracy
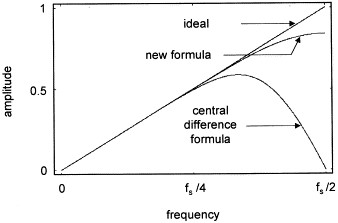
This topic has many interesting facets. During a literature search, I found a 20-year old paper[4] that describes a new set of differencing formulas for ND – when I implemented them in APL, they turned out to have superior accuracy. In fact, when compared to the ND routines in the GNU Scientific Library (GSL), the new approximations are consistently more accurate – up to 13 or 14 significant digits vs. 9 or 10 for GSL. The accuracy on both Multiple-Precision FP and Ball Arithmetic numbers is even more impressive because there the precision can be increased so as to deliver a result with exactly the desired precision.
I became convinced that this algorithm was worth investigating when I saw the following “worth a thousand words” picture in the original[4] paper:
Classification
This algorithm is in the class of ND differencing algorithms, all based on Taylor series[5] expansions. This type of algorithm samples nearby points around the target point x, evaluates the function at these points, differences them in pairs, weights those differences, and then adds them together to achieve the final result. For example, the first order approach is to calculate f(x+h) – f(x-h) all divided by 2h, where h is some small number. This means the function is sampled at two points x±h, differenced (subtract one from the other) and weighted by 1/2h. The parameters to this algorithm are the Sampling Frequency (h, the radius around x) and the Sample Size (number of points, e.g. x±h, x±h/2, x±h/4, etc.). All ND differencing algorithms use some variation on this template.
APL Code
The (origin-1) APL code to implement this algorithm is as follows:
The three values below are used to bridge the difference between even and odd degrees of the Derivative.
c←⌊(p-1)÷2 ⋄ c1←0=2|c ⋄ c2←0=2|p
The following lines calculate into tab the weights on the sample values. These calculations are stored entirely in a static table in the library code. The Variant operator on the Factorial function implements a Pochhammer Symbol[6] which is a generalization of Double Factorial as in !!(2N-1) = (2N-1)×(2N-3)×(2N-5)…1.
X←×/¨(⊂[2]010 2‼c (N-1))∘.(⌷¨)⊂¨(¯1+2×(⊂⍳N)~¨⍳N)÷2 X←+⌿X*¯2 j←(1-N)..N Cnj←((!⍠((-N)2)¯1+2×N)*2)÷(4*N)×(!N-j)×!N+j-1 tab←(¯1*j+c1)×((!p)÷((¯1+2×j)÷2)*2+c2)×Cnj×(⌽X),X
All of the lines above (including the calculation of c, c1, and c2) are part of the static tables when calculated across all relevant p and N as a p by N matrix of length 2×N vectors. In this implementation, I chose p←1..9 and N←1..7. In practice, the above calculations are all done as Rational Numbers so as not to lose precision were they to be done in Floating Point.
The following three lines constitute the entire algorithm exclusive of generation of the static tables:
Call the function on the 2×N Sample Values spaced apart by T around R weighting the result by the appropriate 2×N length vector from tab.
w←p N⊃tab ⋄ Z←w+.×F R+T×(¯1+2×(1-N)..N)÷2
The sum of the weights is 0 for odd degrees. For even degrees that sum is the weight on the value of the function at the center point whose product is subtracted from the weighted sum above.
:if 0=2|p ⋄ Z-←(+/w)×F R ⋄ :end
Finally, scale the result by T for each degree of the derivative.
Z÷←T*p
where F is the function whose derivative is being calculated, N is the Order (Sample Size), p is the Degree (1st, 2nd, 3rd, etc.), and T is the Sampling Frequency (10SFE) of the Derivative.
Benefits
Delightfully, this paper (along with two related papers[7], [8] from the same authors) provides a number of benefits:
- The algorithm is quite simple as seen above
- Because it is so simple, it extends easily to
- Double-Precision FP numbers
- Multiple-Precision FP numbers
- Ball Arithmetic numbers
- Varying sample sizes and spacing
- Higher degrees such as 2nd, 3rd, 4th derivative, etc.
- Hypercomplex numbers
I have finished implementing all of this except the extension to Hypercomplex numbers. The latter looks doable, but I don’t understand the theory as yet. Interestingly, the degree of the Derivative is obtained simply by counting the number of occurrences of ∂ in the Left Operand. This number is passed to the basic library routine which uses it (along with the Order) as an index into a two-dimensional array (p by N) of vectors of length 2×N to obtain the weights on the values of the function at the 2×N sampling points. Because the Degree is used solely as an index to an array to retrieve a vector of weights, there is no performance impact whatsoever for using one Degree over another.
I intend to contribute these algorithms (already written in C) to each of the GSL, MPFR, and ARB open source libraries.
Forward and Backward Differencing
Central Differencing samples points on both sides of a center point which works fine for a function everywhere defined. However if you need a derivative of a function undefined above or below a certain point and you need the derivative at or near that point, Central Differencing won’t work.
Forward differencing samples the values of the function at or above the given point, never below. For example, in the set of Real numbers, the square root of X is undefined below 0, and so if you want to calculate a derivative of that function at 0, you’ll need Forward Differencing. Backward Differencing is simply the dual to Forward Differencing.
At the moment, only Central Differencing is implemented, but this might be extended in the future.
Variants
The Variant operator has been extended to the ND operator so as to gain access to finer control of the algorithm. In particular, it may be used to override the default Order (5) of the derivative as well as the Sampling Frequency as in f∂⍠(Ord SF) R, where Ord must be first, SF second. To override just the Order, use f∂⍠Ord R. To change the Sampling Frequency Exponent but not the Order, use 0 for the Order.
For example, trying several different Orders:
⎕FPC←128 ⋄ ⎕PP←40
!∂⍠4 0v
¯0.577215664901532860606512090081972171634
!∂⍠5 0v ⍝ Default Order
¯0.577215664901532860606512090082402425136
!∂⍠6 0v
¯0.577215664901532860606512090082402403875
!∂⍠7 0v
¯0.577215664901532860606512090082402444579
¯1g1v ⍝ Exact value
¯0.577215664901532860606512090082402431043
For this example at least, Order 5 provides a marked improvement over the previous Order without much improvement above that.
The default Sampling Frequency Exponent is
SFE←-⌊0.5+⎕FPC÷32
which translates to a Sampling Frequency of
SF←10*SFE
This value is used as the spacing between Sample Values passed to the function. The SFE may be overridden as described above.
Forward and Backward Differencing may be specified by including a character scalar anywhere in the Right Operand of the Variant operator. The possibilities are 'b', 'f', and 'c' for Backward, Forward, and Central Differencing. However, at the moment, only Central Differencing is implemented in the new code.
For reference, the original Order 2 ND code from GSL is available through the Variant operator by using the uppercase letter in the above list. The GSL code implements all three forms of Differencing, and has been translated into both Multiple-Precision Floating Point and Ball Arithmetic.
For example,
!∂⍠'C' 0 ⍝ GSL code ¯0.5772156648930862 !∂⍠'c' 0 ⍝ New code ¯0.5772156649015363 !∂⍠'C' 0± ⍝ GSL Ball code ¯0.577215664901532860606512052695926256206±2.2E¯24 !∂⍠'c' 0± ⍝ New Ball code, same as !∂0± ¯0.577215664901532860606512090082402327882±1.6E¯33 ¯1g1v ⍝ Exact value ¯0.577215664901532860606512090082402431043
Implementation
The algorithm described in the I.R. Khan, R. Ohba paper[8] has been translated three times once for each of the three floating point datatypes: Double-precision, Multiple-precision, and Ball Arithmetic. Consequently, your result is dependent upon the datatype of the argument you supply. For example,
⎕FPC←128 ⍝ Working precision
!∂0 ⋄ !∂0x ⋄ !∂0± ⋄ ¯1g1x
¯0.5772156649015363
¯0.577215664901532860606512090082402431128
¯0.577215664901532860606512090082402327882±1.6E¯33
¯0.577215664901532860606512090082402431043
which shows that the accuracy and precision of the result depends upon both the working precision and the argument's datatype (i.e., algorithm).
Also, to achieve better performance, all three algorithms use an internal table of coefficients for Degree vs. Order limited to the indices p←1..9 and N←1..7. For the Multiple-precision and Ball Arithmetic algorithms, if either the user-specified Degree or Order is outside the original table limits, a separate algorithm is used to calculate the correct coefficients — and so those two algorithms are not constrained by the limits of the internal tables.
Idioms and Inverses
An extension to this approach to ND is one taken by J which first attempts to recognize the ND operator’s Right Operand function as an idiom by looking up its derivative in a table and, if successful, execute the derivative function directly on the argument. For example, the derivative of sine (1○⍵) is cosine (2○⍵), easily resolved by a table lookup. Failing that, numerically differentiate the function.
A successful table lookup can both speed up the calculation and improve the accuracy of the result. Moreover, higher degree derivatives can be calculated through iterative table lookups.
Another opportunity for idiom recognition used by J is when evaluating the inverse of the Derivative which is expressed in APL as {⍺←0 ⋄ ⍺ ⍺⍺∂⍣¯1 ⍵} or more directly as {⍺←0 ⋄ ⍺ ⍺⍺∫⍵}.
These excellent ideas are on my list of future work.
Partial Derivatives
In mathematical notation, Partial Derivatives are expressed w.r.t a variable in a multiple variable expression as in ∂f/∂x where f is some function of multiple variables one of which is x.
In APL, we don't have multiple variables, but we do have multiple elements in an array argument to the Derivative operator where the function Operand also returns multiple values. This concept is explained more clearly in Iverson[2] and Powell[3].
For example, from Iverson[2],
{+/⍵∘.×⍵}∂1 2 3
7 1 1
2 8 2
3 3 9
where the rows in the result represent the several components of the function and the columns represent the set of the Partial Derivatives of component functions of the several variables in the argument.
Numerical Integration
Note that Numerical Integration, the inverse of this operator, has also been implemented.
Acknowledgements
This feature is entirely based on several papers of I.R. Khan, R. Ohba[4][7], in particular their one on Taylor series[8] expansions.
References
- ↑ NARS2000 Wiki, "Matrix Operator" [1]
- ↑ 2.0 2.1 2.2 "The Derivative Operator", Kenneth E. Iverson, APL '79: Proceedings of the international conference on APL: part 1, May 1979, pp. 347–354[2]
- ↑ 3.0 3.1 "The Derivative Revisited", Mike Powell[3]
- ↑ 4.0 4.1 4.2 “New Finite Difference Formulas for Numerical Differentiation”, I.R. Khan, R. Ohba / Journal of Computational and Applied Mathematics 126 (2000) pp. 269-276
- ↑ Wikipedia, “Taylor Series”, https://en.wikipedia.org/wiki/Taylor_series
- ↑ NARS2000 Wiki, “Variant – Rising and Falling Factorials”, http://wiki.nars2000.org/index.php/Variant#Rising_and_Falling_Factorials
- ↑ 7.0 7.1 “Closed-form Expressions for the Finite Difference Approximations of First and Higher Derivatives Based on Taylor Series”, I.R. Khan, R. Ohba / Journal of Computational and Applied Mathematics 107 (1999) pp. 179-193
- ↑ 8.0 8.1 8.2 “Taylor Series Based Finite Difference Approximations of Higher-Degree Derivatives”, I.R. Khan, R. Ohba / Journal of Computational and Applied Mathematics 154 (2003) pp. 115-124